[그래프이론] 2. DFS 깊이우선탐색

in Algorithm on Dfs, Graph

BFS와 함께 그래프 탐색시 가장 많이 쓰이는 알고리즘이 DFS(Depth-First Search), 깊이우선탐색입니다. 많은 문제를 풀면서 각 알고리즘을 손에 익혀두지 않으면 실전에서 당황하기 십상이기 때문에 DFS를 이용한 탐색 방법을 정확히 익혀두고, 문제를 많이 풀어서 문제에 맞는 알고리즘을 그때그때 선택해야합니다.

BFS가 시작노드로부터 떨어진 거리순(1 → 2 → 3 …)으로 그래프를 탐색하는 기법이라면, DFS는 ‘갈 데까지 가보는(?)’ 방식으로 그래프를 탐색합니다. 풀어서 설명하면 갈 수 있는 데까지 깊이 가보다가 더이상 탐색할 노드가 없으면 그때 다시 돌아가서 다른 노드를 탐색합니다.

그림으로 살펴보면 다음과 같습니다.

0부터 5까지의 숫자가 적힌 노드들이 있고, 탐색이 시작되는 노드는 0입니다. 이 노드들은 모두 가중치가 1로 동일한 양방향 간선으로 연결되어 있습니다. (간선에 적힌 숫자는 간선의 가중치가 아닌 시작노드(0)로부터 각 노드까지의 거리를 뜻함)

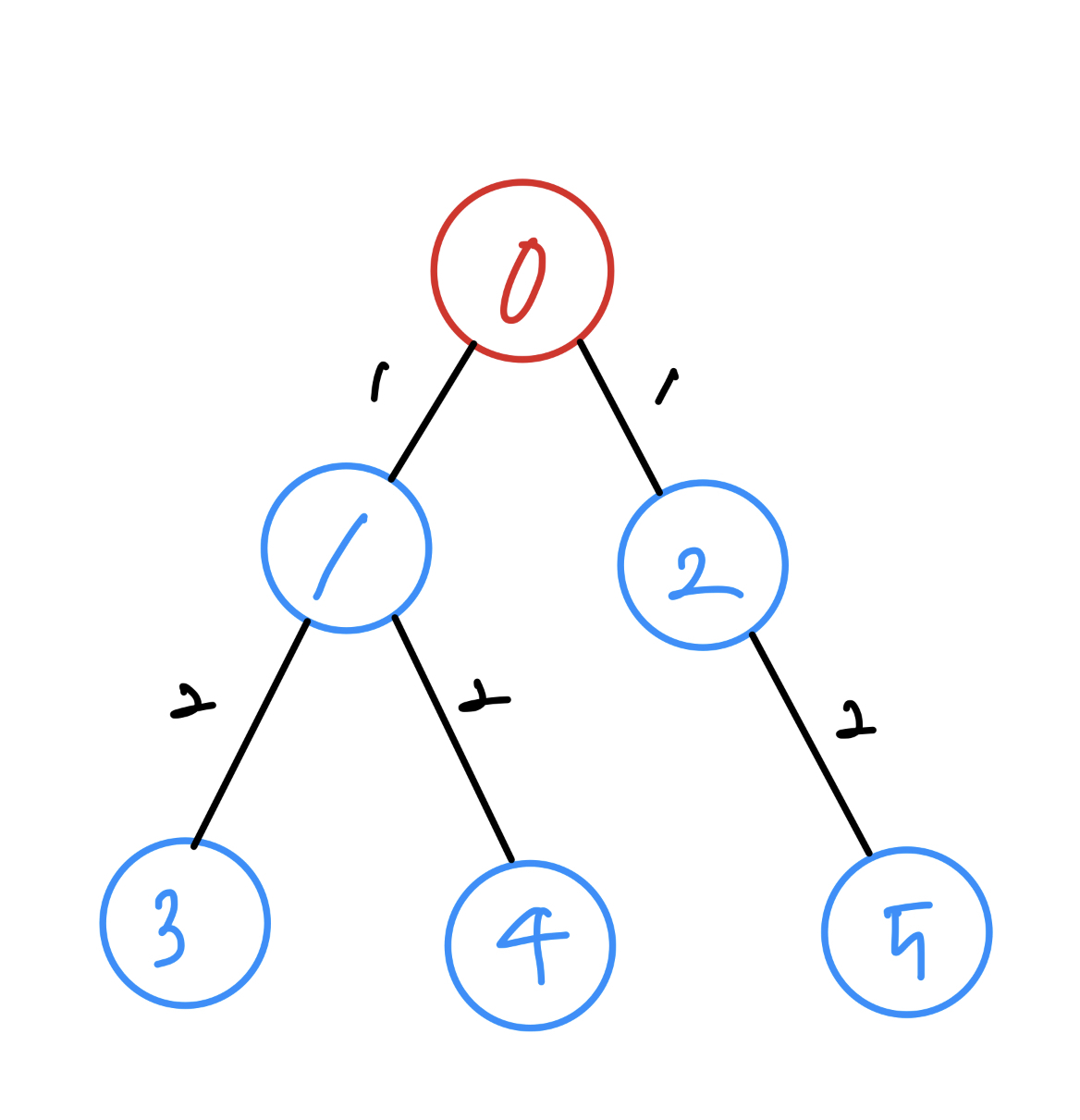
image

우선, 시작노드에 가장 가까이 있는 노드부터 탐색하되, 그런 노드들이 여러개 있으면 노드에 적힌 수가 가장 작은 것부터 시작합니다. 1, 2 중 1부터 탐색을 시작합니다.

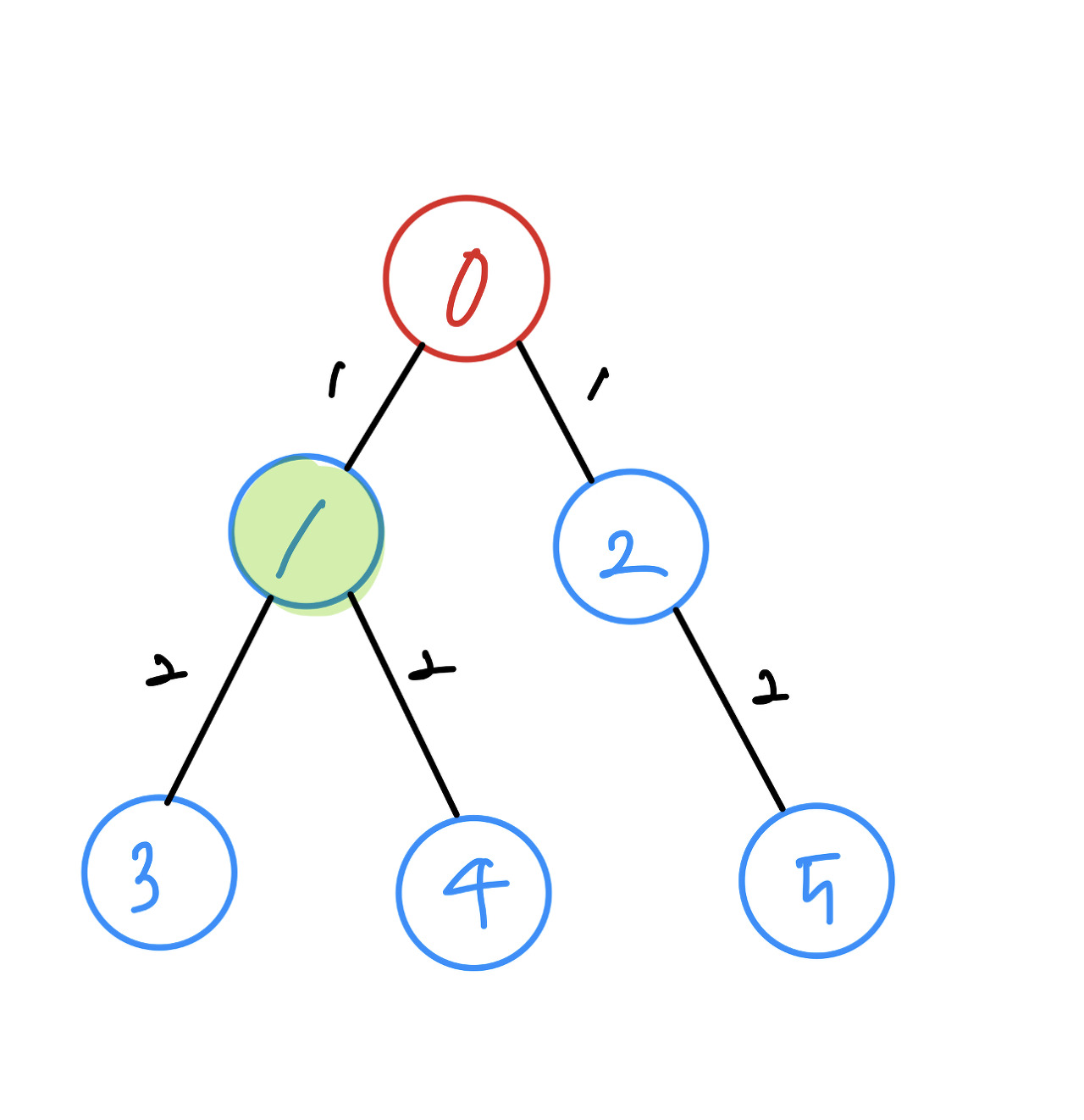
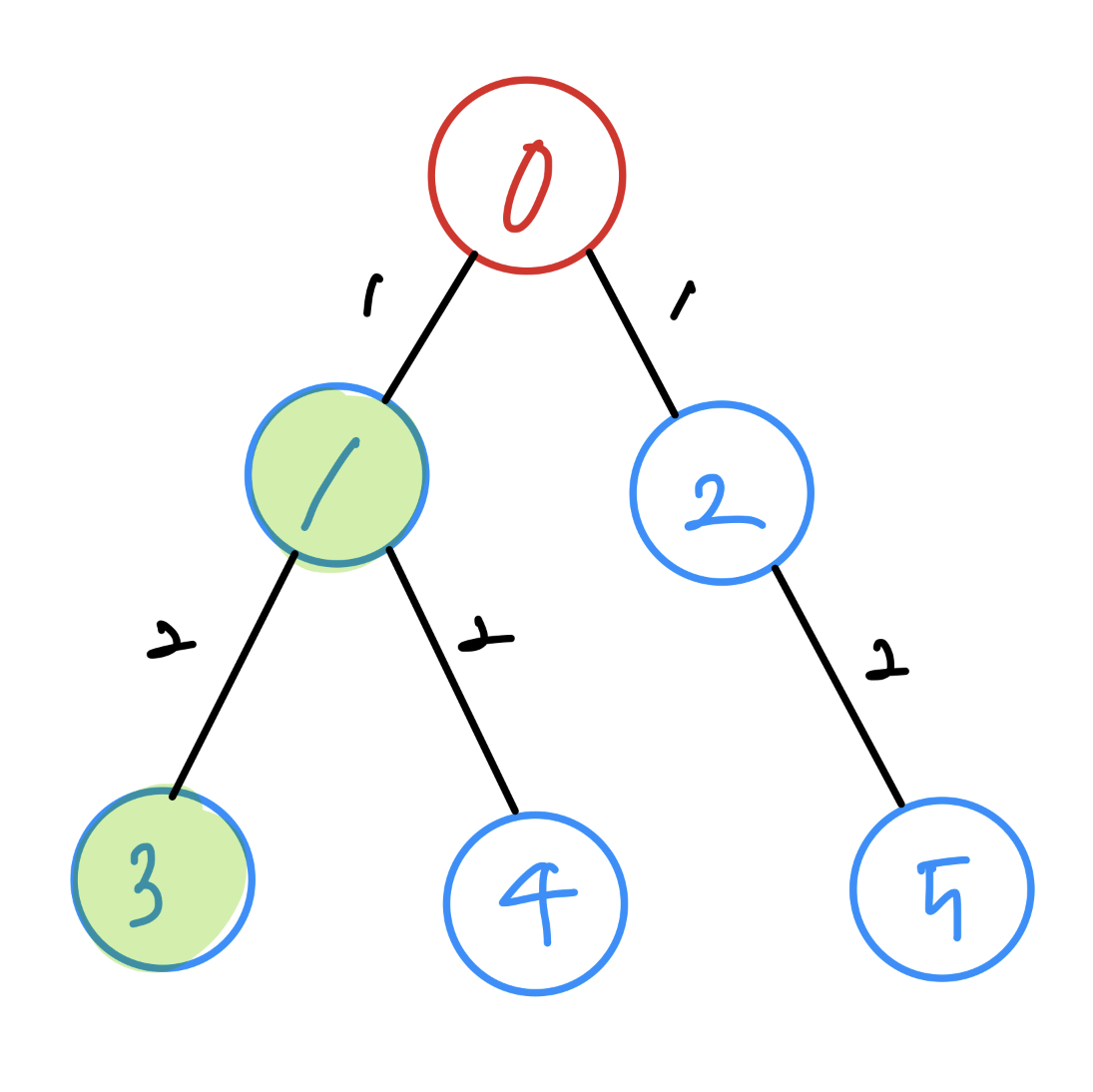
image image

DFS는 ‘갈 수 있는 데까지 깊이 가보는 그래프탐색기법’이라고 했습니다. 이전에 탐색한 노드에 연결된 노드를 타고 계속 타고 가보다가, 갈 수 없으면 한단계 돌아와서 다시 탐색 가능한 노드가 있는지 살펴보는 것이 DFS입니다. 1을 처음에 탐색했기 때문에 1에 연결된 노드를 타고 들어갑니다. 3, 4 중 숫자가 작은 3을 탐색합니다.

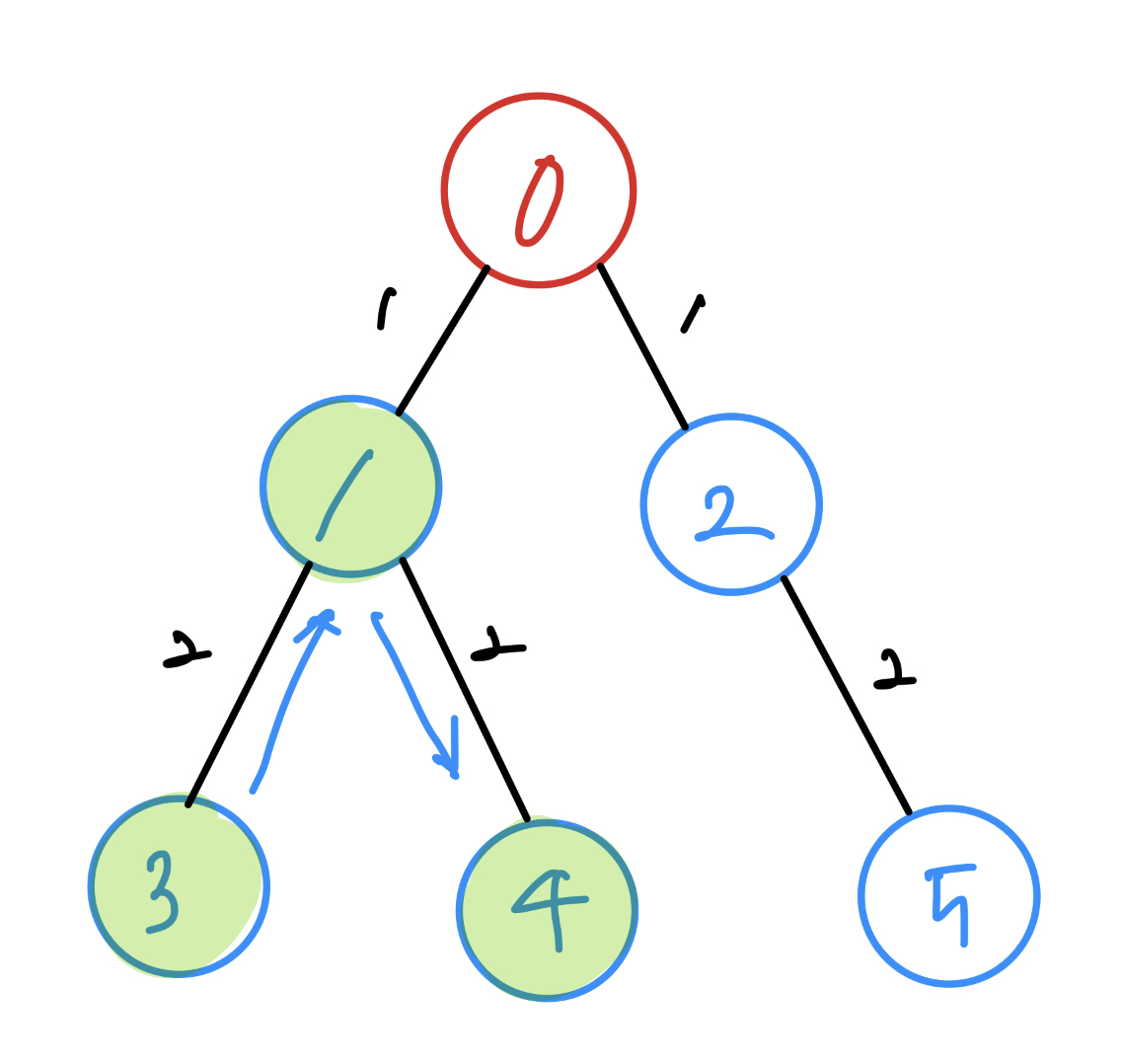
image

방금 3을 탐색했는데, 3에서 더 타고 들어갈 수 있는 노드는 없습니다. 3과 연결된 노드1이 있지만, 이전에 탐색했기 때문에 대상에서 제외합니다. 갈 데까지 갔기 때문에 1로 돌아옵니다. 그리고 1과 연결되어있고, 아직 탐색하지 않은 4를 탐색합니다.

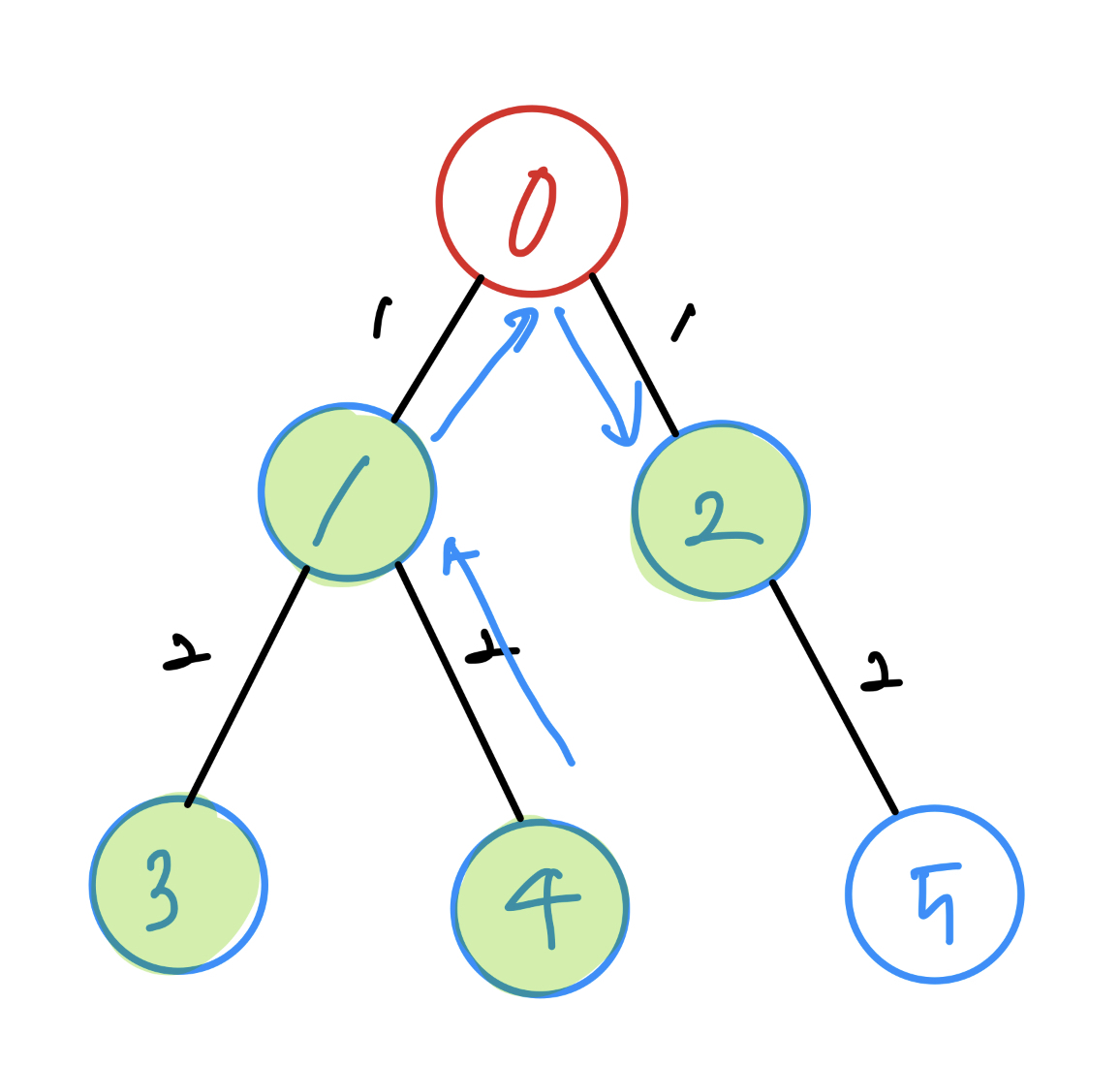
image

깊이는 다르지만 원리는 같습니다. 4를 탐색한 후 4와 연결된 노드 중 아직 탐색하지 않은 노드가 없기 때문에 1로 돌아옵니다. 마찬가지로 1과 연결된 노드 중 아직 탐색하지 않은 노드가 없기 때문에 0으로 돌아옵니다. 0(시작노드)과 연결된 노드 중 아직 탐색하지 않은 노드 2가 있죠. 2를 탐색합니다.

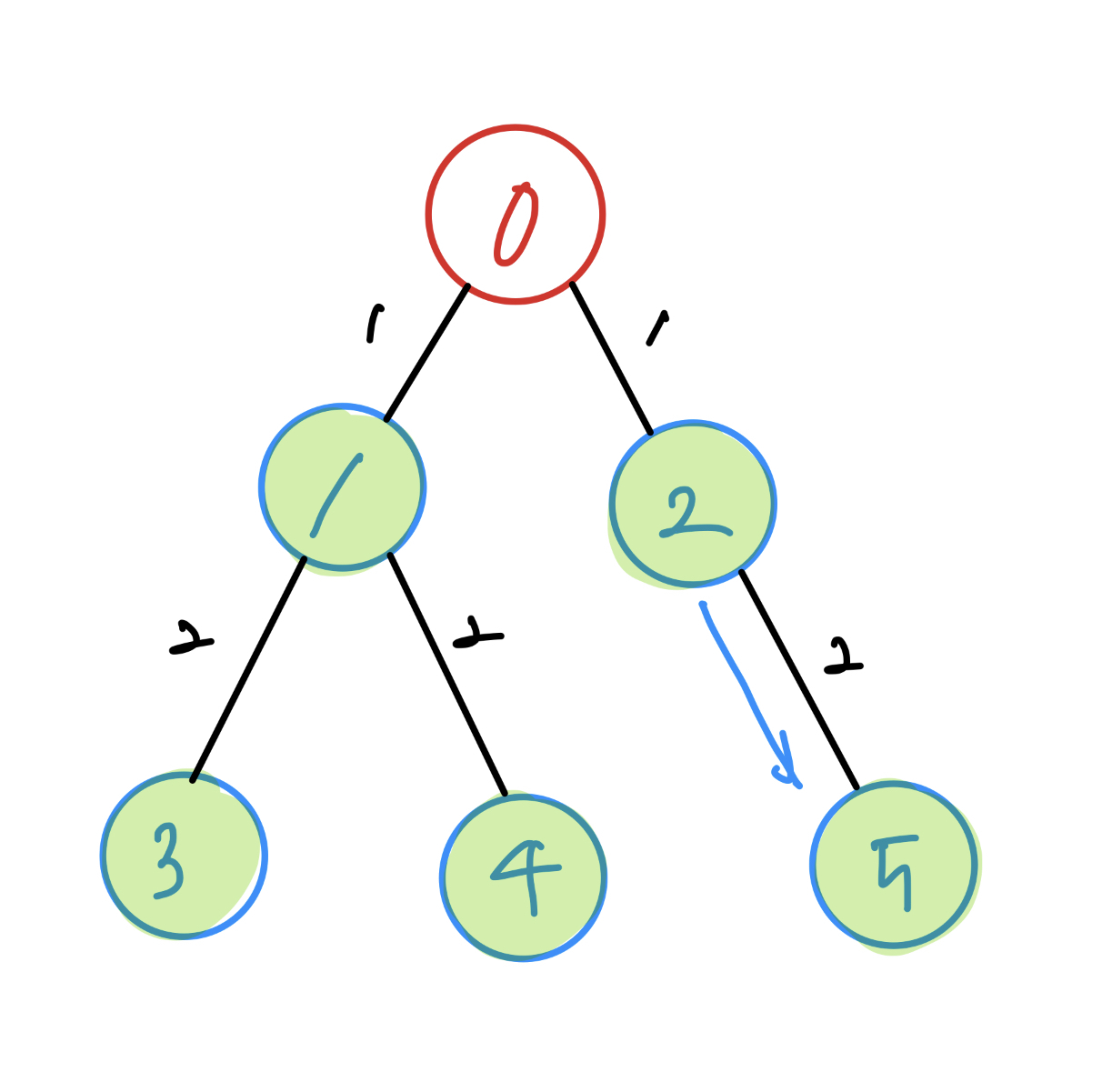
image

똑같은 원리로 5를 탐색합니다. 이후엔 어떻게 될까요. 더이상 탐색할 노드가 없기 때문에 5 → 2 → 0 (시작노드)로 돌아온 후 탐색이 종료됩니다.

이런 원리 때문에 ‘갈 데까지 가는 탐색방식’이라고 설명드린겁니다ㅋㅋㅋ. BFS를 구현할 때에는 거리순으로 방문하기 때문에 queue 자료구조를 사용했는데요, DFS에서는 어떤 자료구조를 사용해야 할까요. 노드에 연결된 노드들을 타고 들어갔다가, 다시 빠져나오는 방식의 기법이기 때문에 stack을 사용합니다. 또는 재귀를 사용해 구현할 수 있습니다. 대부분의 문제를 재귀를 사용해 구현해 해결합니다.

방금 그림으로 살펴본 예시를 코드로 구현해보겠습니다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

class Graph {
public:
    int N;
    vector<vector<int>> adj; // 인접리스트 : 노드간 연결 여부를 기록
    vector<bool> visited; // 방문여부를 체크하는 배열

    // 생성자
    Graph() {}
    Graph(int n) {
        N = n;
        adj.resize(n);
        visited.resize(n);
    }

    // 간선추가 함수
    void addEdge(int a, int b) {
        adj[a].push_back(b);
        adj[b].push_back(a);
    }

    // 모든 인접리스트의 정점 번호를 정렬
    void sortAdjList() {
        for (int i = 0; i < N; i++) {
            sort(adj[i].begin(), adj[i].end());
        }
    }

    // dfs
    void dfs(int curr) {
        visited[curr] = true; // 노드 방문 체크
        cout << "node " << curr << " visited" << endl; // [노드탐색 순서 체크용]
        for (int next: adj[curr]) { // curr에 연결된 노드들 중 
            if (!visited[next]) dfs(next); // 아직 방문되지 않은 노드들있으면 탐색
        }
    }
};

int main() {
    Graph g(6);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 5);

    g.dfs(0);
    
    return 0;
}

// <result>
// node 0 visited
// node 1 visited
// node 3 visited
// node 4 visited
// node 2 visited
// node 5 visited

BFS와 마찬가지로 DFS도 격자판이 등장하는 문제가 많아서 단순 노드들로 구성된 그래프 문제뿐만 아니라 격자가 나오는 문제를 많이 다뤄보셔야할 것 같습니다.

참고

  • Ries 마법의 슈퍼마리오(https://m.blog.naver.com/PostView.naver?blogId=kks227&logNo=220785731077&referrerCode=0&searchKeyword=dfs)
  • [알고리즘 트레이닝] - 안티 라크소넨