[그래프이론] 1. BFS 너비우선탐색

in Algorithm on Bfs, Graph

BFS(너비우선탐색)는 DFS(깊이우선탐색)과 마찬가지로 그래프를 순회하기 위한 알고리즘입니다. BFS와 DFS는 시작 노드(node)와 연결된 노드들을 모두 순회한다는 점에서 DFS와 동일하지만, 순회방법 및 순서에 있어 차이점이 있습니다.

DFS와 관련된 내용은 다음 포스팅에서 다루기로 하고, 오늘은 BFS에 대해 정리하겠습니다.

그래프 관련 용어 정리

BFS/DFS를 설명하기 전에 ‘그래프’에 대한 이해가 좀 필요합니다. BFS와 DFS의 기본 개념을 이해하기 위한 그래프 용어를 정리해보겠습니다.

그래프(graph)는 노드(node, vertext(정점)이라고도 합니다)와 그들을 잇는 간선(edge)로 구성되어 있습니다. 한 노드에서 그래프의 간선을 지나 다른 노드까지 가는 길을 경로(path)라고 하고, 처음 노드와 마지막 노드가 같은 경로를 사이클(cycle)이라고 합니다.

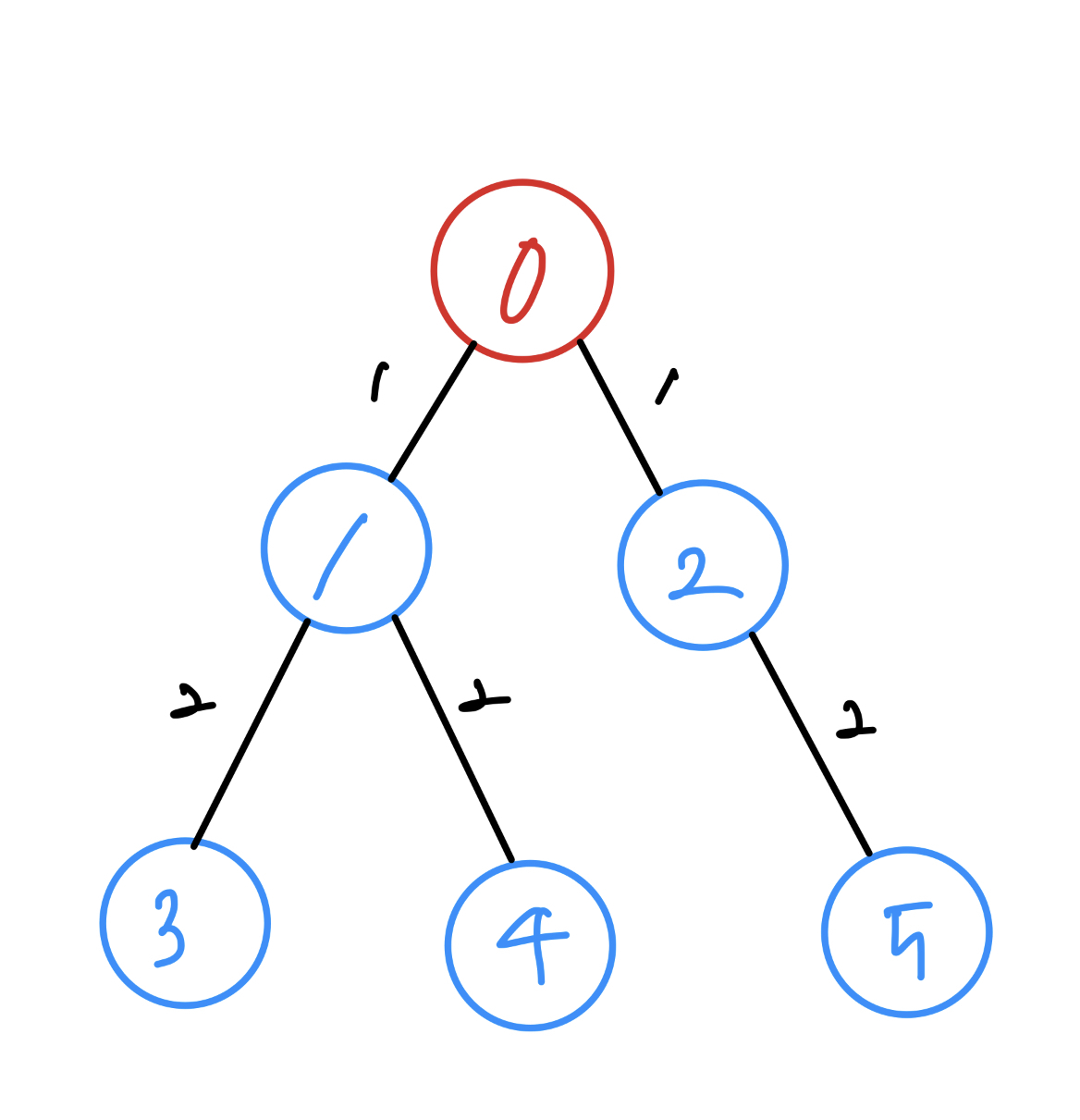
image

위 그림은 0~5까지의 수를 가지는 노드와 노드들을 잇는 간선을 표현한 그림입니다. 간선에 적힌 수는 모든 간선이 1의 거리를 가진다고 할 때, 0이 적힌 노드에서 다른 노드까지의 거리를 나타냅니다.

간선에는 방향과 가중치가 있을 수도 있는데, 두 노드가 간선으로 연결되어 있어도 한쪽에서 다른 한쪽으로 밖에 이동하지 못하도록 방향이 설정되어 있을 수도 있고, 위 그림처럼 모두 동일한 가중치(or 거리)를 가지는 것이 아니라, 다른 가중치를 가질 수도 있습니다.

또한 위 그래프를 보면 모든 노드 간에 경로가 있죠. 이런 그래프를 연결 그래프(connected graph)라고 합니다. 만약 그래프에 있는 한 노드에서 간선을 거쳐 이동할 수 없는 노드가 있다면 연결 그래프가 아닙니다. 이렇게 연결된 부분을 컴포넌트(component)라고 하는데, 한 그래프에 여러개의 컴포넌트가 있을 수도 있습니다.

BFS, 너비우선 탐색

BFS의 가장 큰 특징은 시작 노드와 직/간접적으로 연결된 다른 노드들을 거리순으로 방문한다는 것입니다. 위 그림은 0에서 5의 값을 가지는 서로 다른 6개의 노드들이 각각 간선으로 연결되어 있습니다. (간선의 가중치는 모두 같은 1로 가정합니다. 간선마다 다른 가중치를 가지는 그래프와 관련한 알고리즘(ex. 다익스트라)도 있습니다만 다른 포스팅에서 다루겠습니다) 간선에 적힌 숫자들은 0의 값을 가지는 노드로부터 1~5까지의 노드들로 이동할 때 거쳐야하는 거리를 표시한 값입니다. 0 → 1로 이동할 때에는 간선을 하나만 이동하면 되므로 1의 거리를 가지고, 3까지 이동할 때에는 1을 거쳐 이동해야하므로 2의 값을 가지는거죠.

앞에서도 언급했듯 BFS는 시작노드와 직/간접적으로 연결된 노드들을 거리순으로 방문합니다. 거리순으로 방문한다는 것은 1의 거리를 가지는 노드 → 2의 거리를 가지는 노드 → 3의 거리를 가지는 노드 … 순으로 방문한다는 뜻입니다.

거리가 같을 경우, 노드에 적혀있는 수가 작을수록 먼저 방문한다(오름차순으로)고 가정하고 예시들어 살펴보겠습니다.

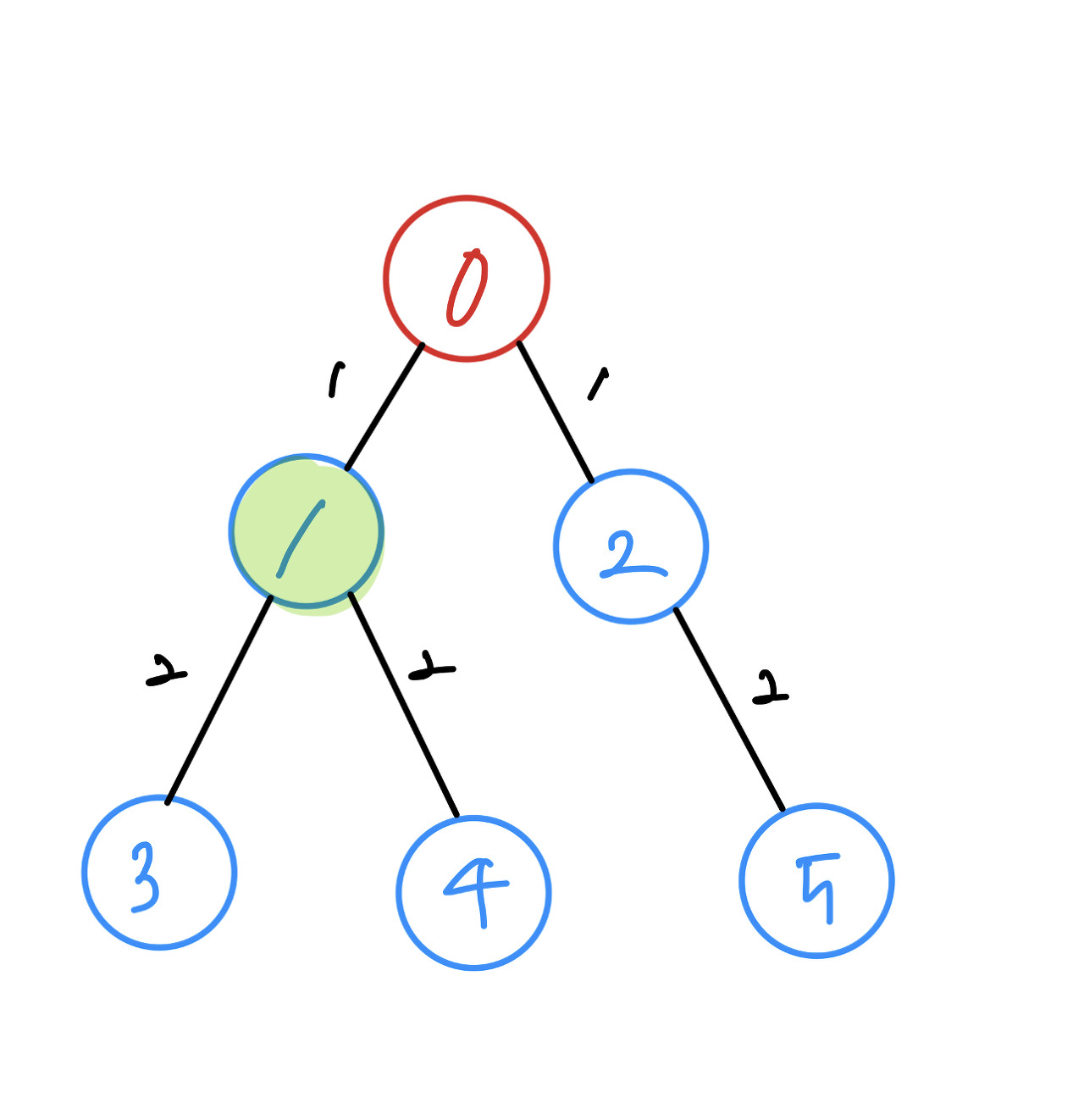
image

거리가 1인 노드가 1, 2 중 노드에 적힌 수가 작은 노드1부터 방문합니다.

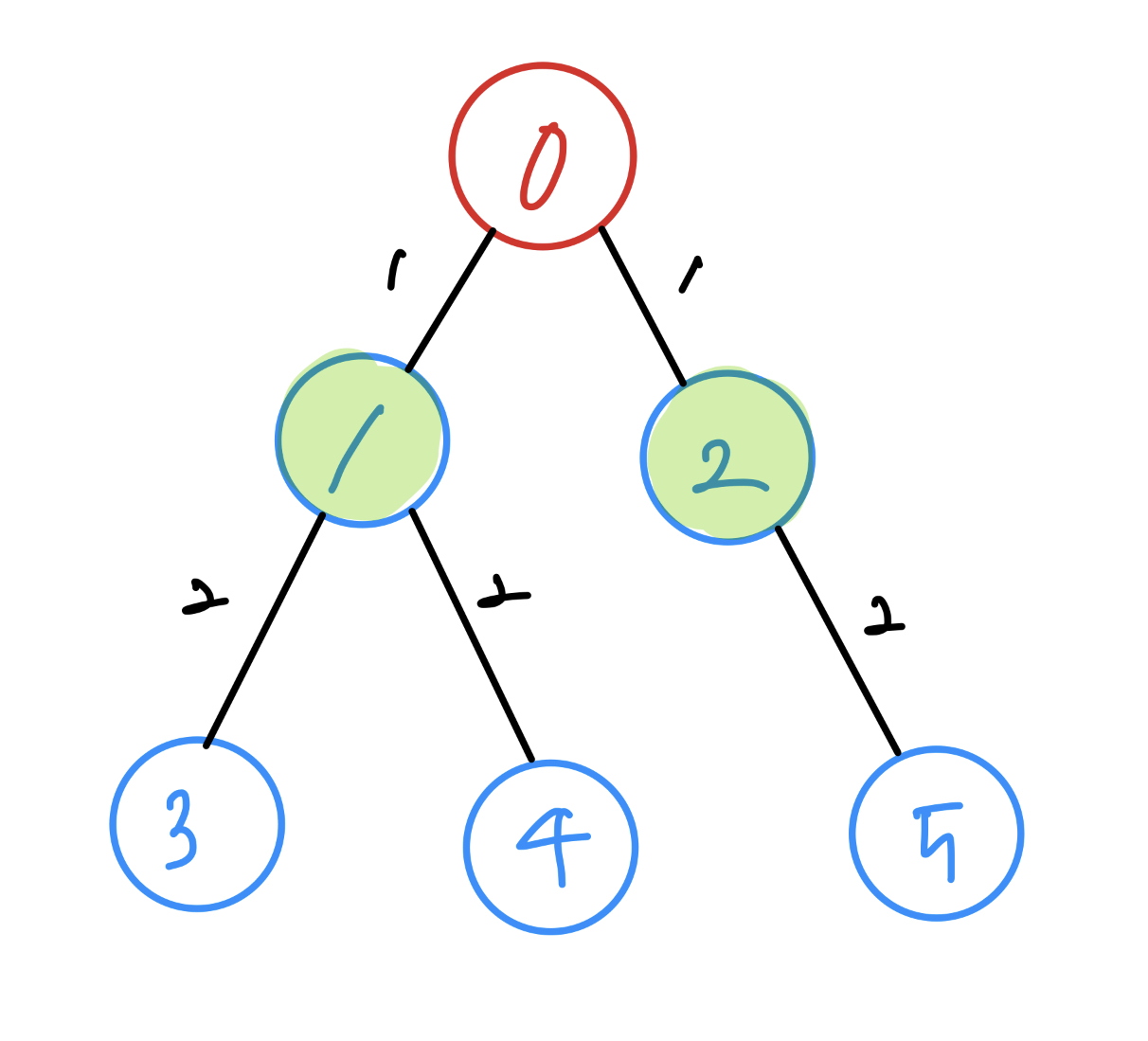
image

그 후 거리가 1인 노드 중 남은 노드2를 방문합니다. 이제 거리가 가장 작은 노드는 방문이 끝났으므로 거리가 2인 노드들을 찾아 방문합니다.

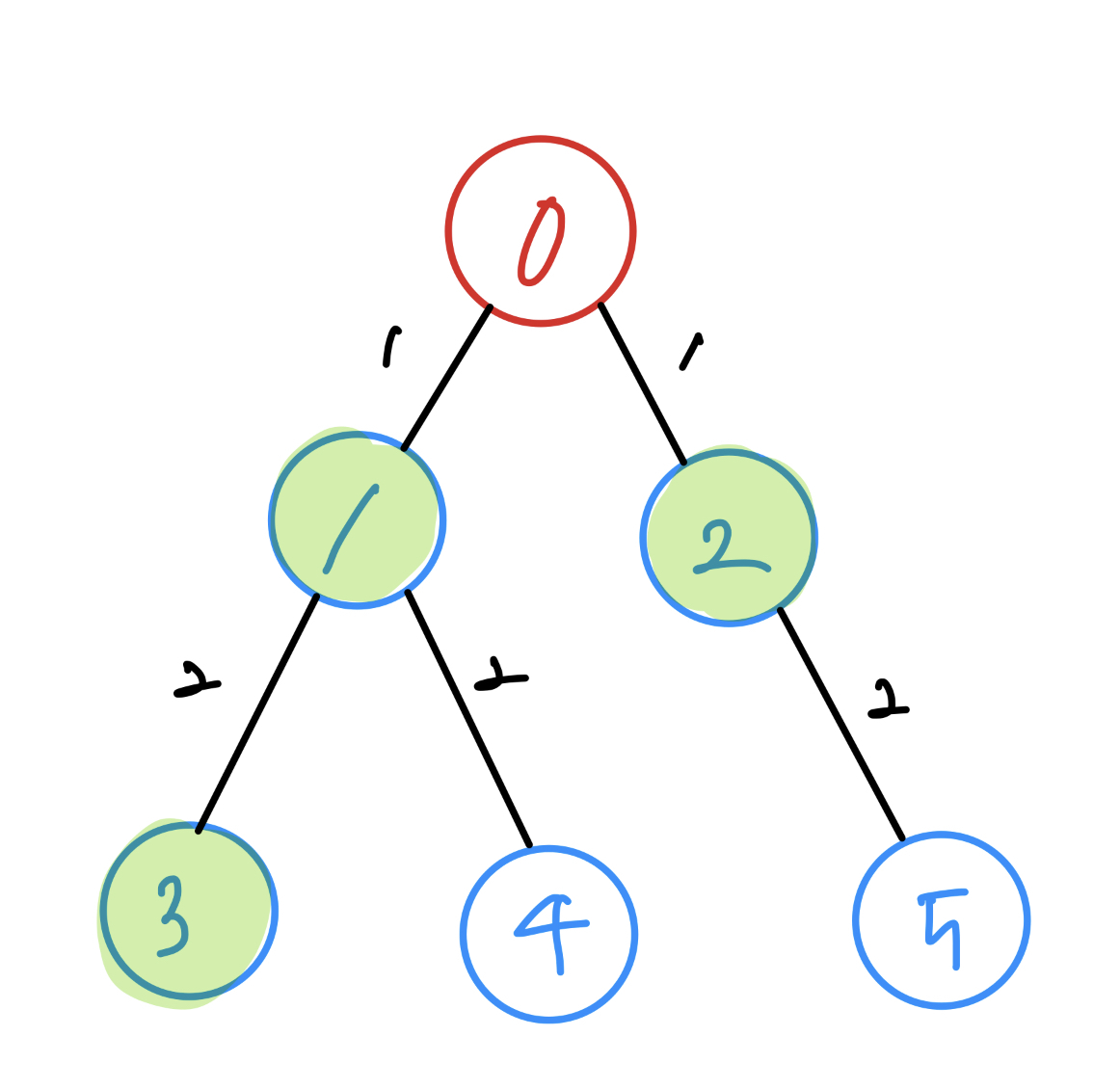
image

먼저 거리가 2인 노드들 중 가장 수가 작은 3을 방문합니다. 그 후 차례로 노드 4, 5를 방문합니다.

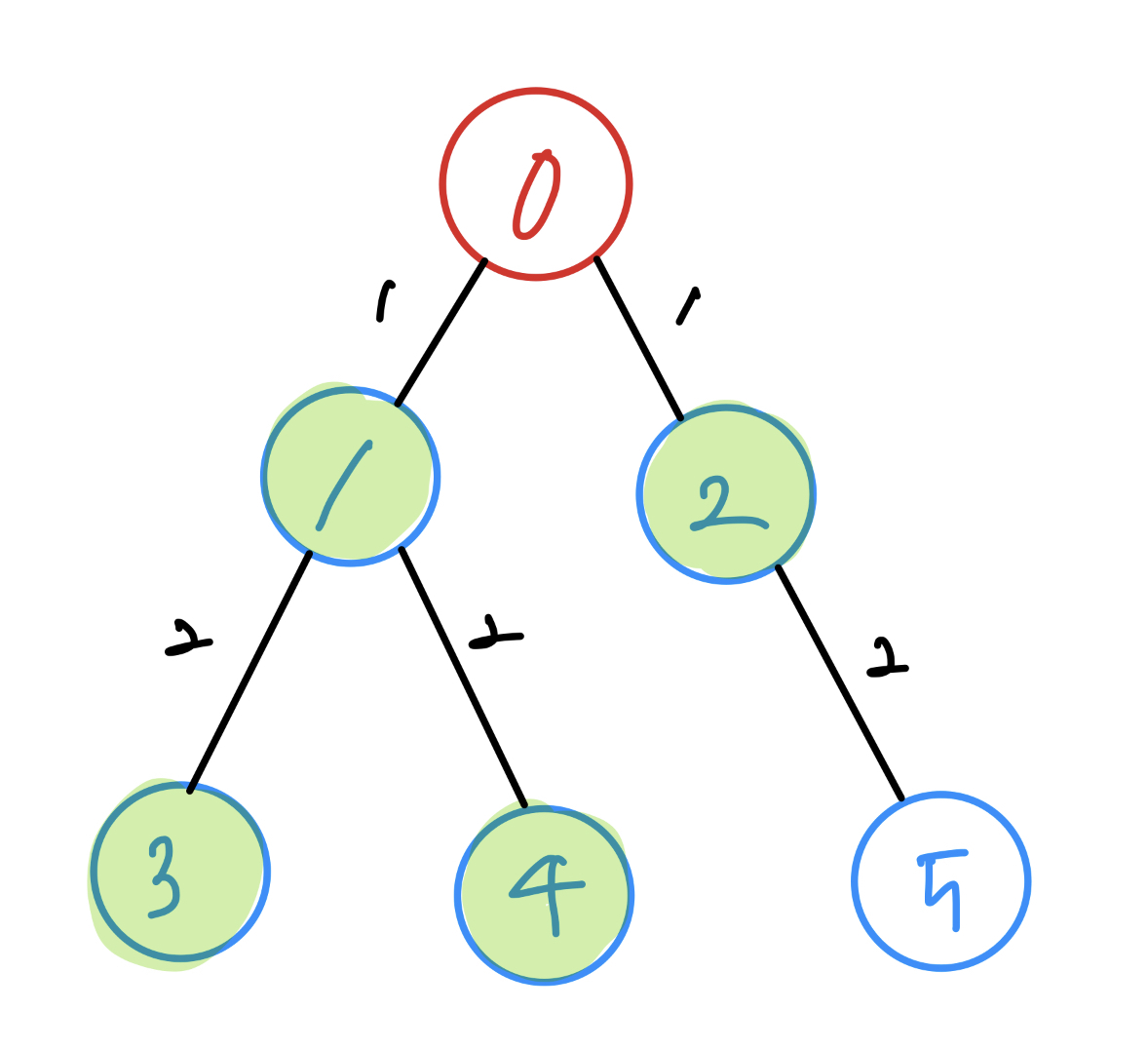
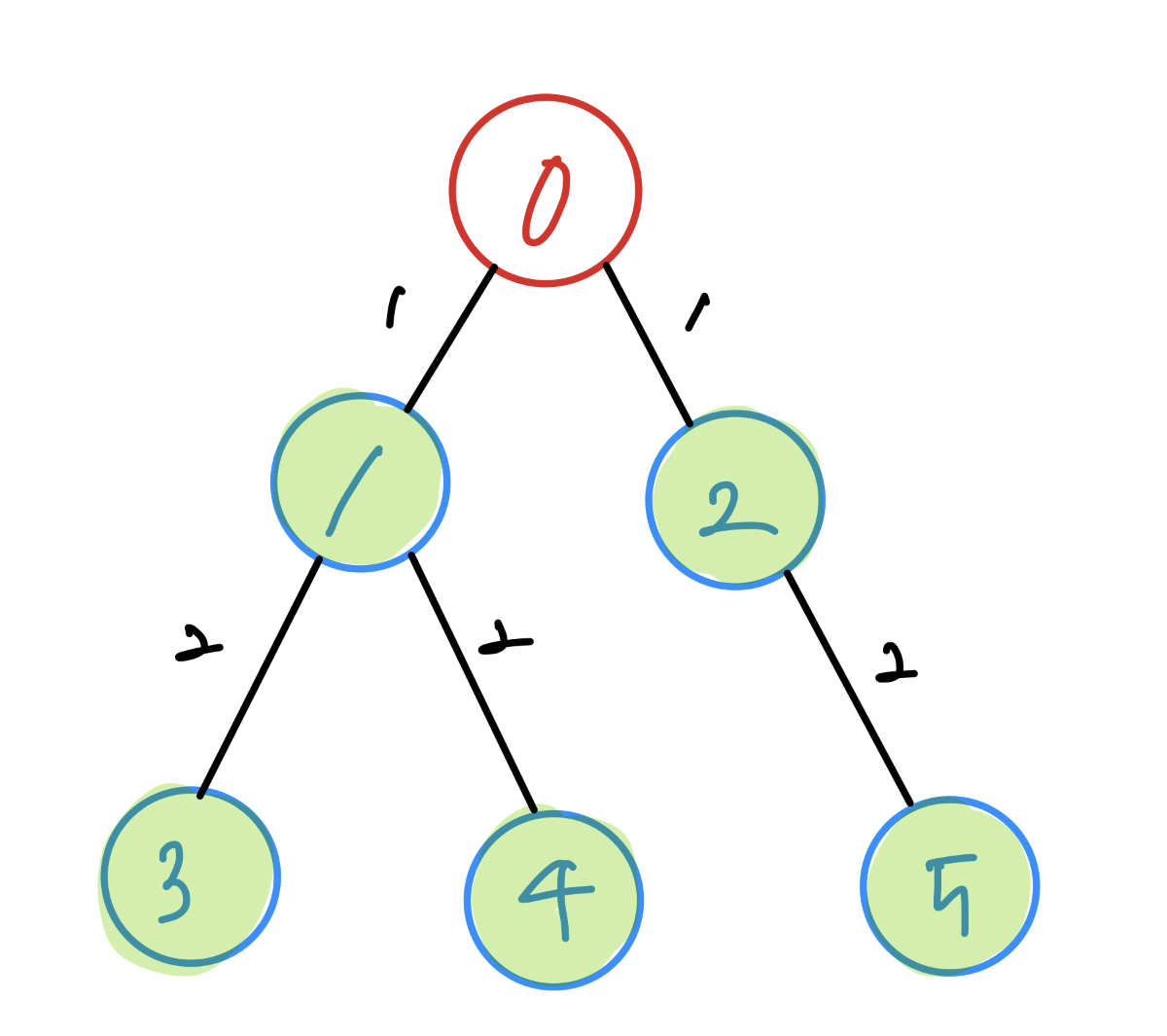
image image

이렇게 5까지 방문하고 나면 노드0에 직/간접적으로 연결된 노드들의 방문이 끝나게 됩니다.

노드0과 연결된 노드들의 방문을 주의 깊에 보면 다음과 같은 순서를 가지는 것을 알 수 있습니다.

  1. 노드0과 연결된 1방문 → 노드0과 연결된 2방문
  2. 노드1과 연결된 3방문 → 노드1과 연결된 4방문
  3. 노드2와 연결된 5방문

방문을 시작하는 노드들과 연결된 다른 노드들을 ‘가까운’ 순서대로 방문하기 때문에, A, B노드가 시작 노드로부터 같은 거리만큼 떨어져 있더라도 A노드와 연결된 노드가 먼저 방문된다면 B노드보다 A노드가 먼저 방문됩니다.

이런 특징을 가지기 때문에 BFS, 너비우선탐색은 Queue(큐)로 구현을 합니다. 방문한 노드들에 연결된 다른 노드들을 Queue에 담고, 다시 Queue에 담긴 노드들 중 가장 빠른(시작노드와 연결된 거리가 짧은) 노드를 꺼내(pop) 탐색을 이어나가는 거죠.

그럼 방금 예시를 통해 설명한 노드들의 탐색을 코드로 나타내보겠습니다.

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

class Graph {
public:
    int N;
    vector<vector<int>> adj; // 인접리스트

    // 생성자
    Graph(int n) {
        N = n;
        adj.resize(N);
    }

    // 간선추가함수(양방향)
    void addEdge(int a, int b){
        adj[a].push_back(b);
        adj[b].push_back(a);
    }

    // 인접리스트의 정점 번호를 정렬
    // 거리가 같을 때 노드에 적힌 번호대로(오름차순) 탐색하기 위함
    void sortNode() {
        for (int i = 0; i < N; i++) {
            sort(adj[i].begin(), adj[i].end());
        }
    }

    // 너비우선탐색 실행
    void bfs() {
        // 방문했던 노드를 체크하기 위한 배열
        // 방문했던 노드를 체크하지 않으면 0 -> 1을 방문했는데 다시 0으로 거슬러 올라가는 등의 중복 방문이 계속해서 발생함
        vector<bool> visited(N, false);

        queue<int> q;
        q.push(0);
        visited[0] = true;

        // 탐색 시작
        while (!q.empty()) {
            int curr = q.front(); q.pop();
            cout << "Node " << curr << "방문" << endl;

            for (int next:adj[curr]) { // curr와 연결된 노드들을 하나씩 살펴봄
                if (!visited[next]) { // next에 아직 방문하지 않았다면 -> 방문
                    visited[next] = true;
                    q.push(next);
                }
            }
        }
    }
};

int main() {

    Graph g(5);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 5);

    g.bfs();

    return 0;
}

BFS문제는 전형적인 시뮬레이션/구현 문제로 많이 등장을 하는데 그런 경우 위 그림과 같은 형태가 아니라 NxN 형태의 격자모양으로 많이 출제가 됩니다. 따라서 격자판의 한칸한칸을 모두 노드로 보고, 그 연결과 탐색을 BFS로 구현하는 연습을 많이 하는 것이 좋겠습니다.

참고

  • Ries 마법의 슈퍼마리오(https://m.blog.naver.com/PostView.naver?blogId=kks227&logNo=220785747864&referrerCode=0&searchKeyword=bfs)
  • [알고리즘 트레이닝] - 안티라크소넨